Ans 17

 

केशनली में उठे द्रव की ऊंचाई का सूत्र

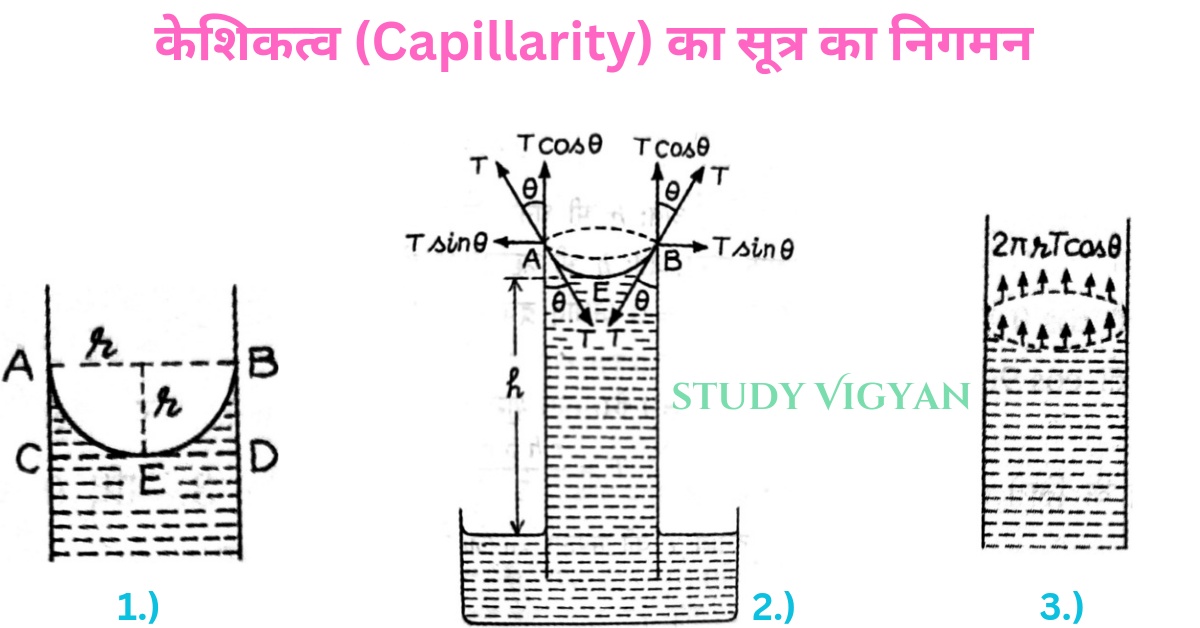
चित्र के अनुसार, कांच की एक स्वच्छ और समान व्यास की केशनली को बर्तन में भरे द्रव में सीधा खड़ा किया गया है।

केशनली में उठे द्रव की ऊंचाई का सूत्र

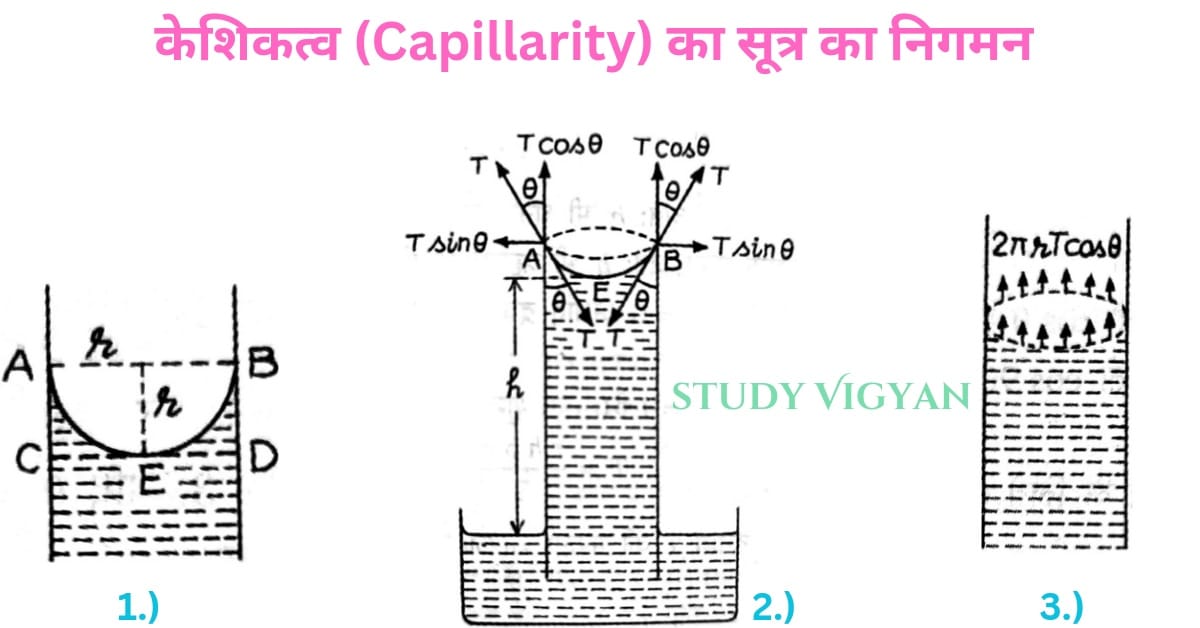
r= केशनली की त्रिज्या है
T= पृष्ठ तनाव (जल या जिस द्रव में केशनली खड़ी है)
h= केशनली में चढ़े द्रव की ऊंचाई
AEB= केशनली में द्रव का नवचंद्रक AEB अवतल है।
2πr= केशनली में द्रव के वक्र पृष्ठ की गोल परिधि

यदि द्रव कांच के लिए स्पर्श कोण θ हो तो यह प्रत्यानयन बल केशनली की दीवार से कोण θ पर द्रव के भीतर की ओर लगता है। केशनली की दीवार भी प्रतिक्रिया के कारण उतना ही बल T द्रव के वक्र पृष्ठ की परिधि की प्रत्येक एकांक लंबाई पर बाहर की ओर लगता है। इस बल के क्षैतिज घटक Tsinθ तथा ऊर्ध्व घटक Tcosθ में वियोजित है।

क्षैतिज घटक Tsinθ परिधि की प्रत्येक प्रत्येक एकांक लंबाई पर बाहर की ओर कार्य करते हैं अतः पूरी परिधि के लिए उनका परिणाम में बल शून्य होगा। ऊर्ध्वाधर घटक T cosθ, परिधि 2πr की प्रत्येक एकांक लंबाई पर ऊपर की ओर कार्य करते हैं

अतः ऊपर की ओर कल आरोपित बल= 2πr × T cosθ

यह बल ही केशनली में चढ़े द्रव के स्तम्भ के भार को संतुलित करता है हमे द्रव स्तंभ के इस भार की गणना करनी है।

केशनली में वक्र पृष्ठ AEB को गोलार्द्ध माना जा सकता है। इसकी त्रिज्या केशनली की त्रिज्या के बराबर है।

अतः केशनली में चढ़े द्रव स्तम्भ का आयतन=
V= h ऊंचाई के बेलन में भरे द्रव का आयतन + नवचंद्रक ACDB में भरे द्रव का आयतन

V= πr²h + (बेलन ABCD का आयतन – गोलार्द्ध AEB का आयतन)

v=πr2h+(πr2(r)−23πr3)

v=πr2h+13πr3

v=πr2(h+r3)

अतः केशनली में चढ़े द्रव का भार= mg = V ρ g =

W=πr2(h+r3)ρg

यहाँ ρ= द्रव का घनत्व
g = गुरुत्वीय त्वरण
द्रव की साम्यावस्था में,
पृष्ठ तनाव पर आरोपित बल = केशनली में चढ़े द्रव के स्तम्भ का भार

2πr×Tcosθ=πr2(h+r3)ρg

अथवा

T=r[h+(r/3)]ρg2cosθ

क्यूंकि r/3 का मान की अपेक्षा बहुत अधिक है, अतः r/3 को h की तुलना में छोड़ सकते है तब-

T=rhρg2cosθ

OR

h=2Tcosθrρg

यही केशिका नली में द्रव के उन्नयन का सूत्र है
(जिसकी मदद से उठे द्रव की ऊंचाई व पृष्ठ तनाव ज्ञात किया जा सकता है)

Important- केशनली जितनी पतली होगी द्रव नली में उतना अधिक ऊंचाई तक चढ़ेगा
ऐसा इसलिए होता है क्यूंकि केशनली की ऊंचाई वाले सूत्र में r का मान नीचे है अतः r का मान जितना कम होगा fraction के ऊपर की value उतनी ही अधिक आएगी

Note-

1. यदि θ<90° होगा तो h भी धनात्मक होगा अतः द्रव नली में ऊपर की ओर चढ़ेगा
2. यदि θ>90° होगा तो h भी ऋणात्मक होगा अतः द्रव नली में नीचे की ओर उतरेगा
3. यदि θ=90° होगा तो द्रव नली में बराबर रहेगा अतः न ही उठेगा ओर न ही नीचे गिरेगा